- Published on
【论文分享】|面向长文本的高效Attention基础结构设计
- Authors

- Name
- 陶思睿
- GitHub
- @Siritao
研究背景
- long context length 对 KV cache 空间的大小提出了新的要求。
- test-time inference 的效率高度依赖模型的推理友好性。
研究 scope
- 只考虑基础架构特性,不涉及动态 KV cache 压缩方案。
- 推理友好性主要考虑推理场景下的计算密度、并行度等。
代表方案
- MHA、GQA、MQA
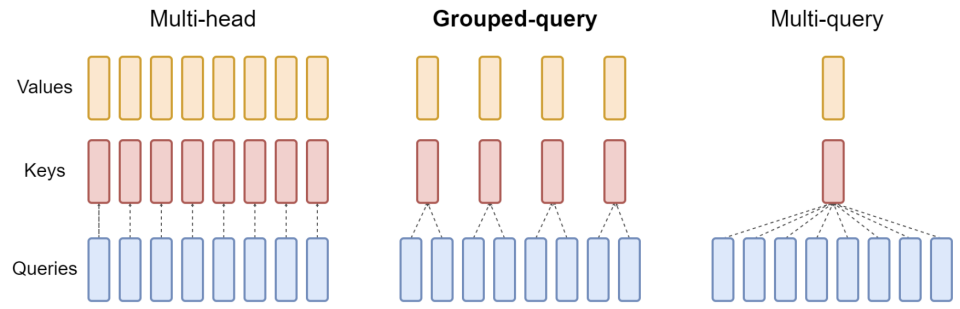
- Deepseek MLA
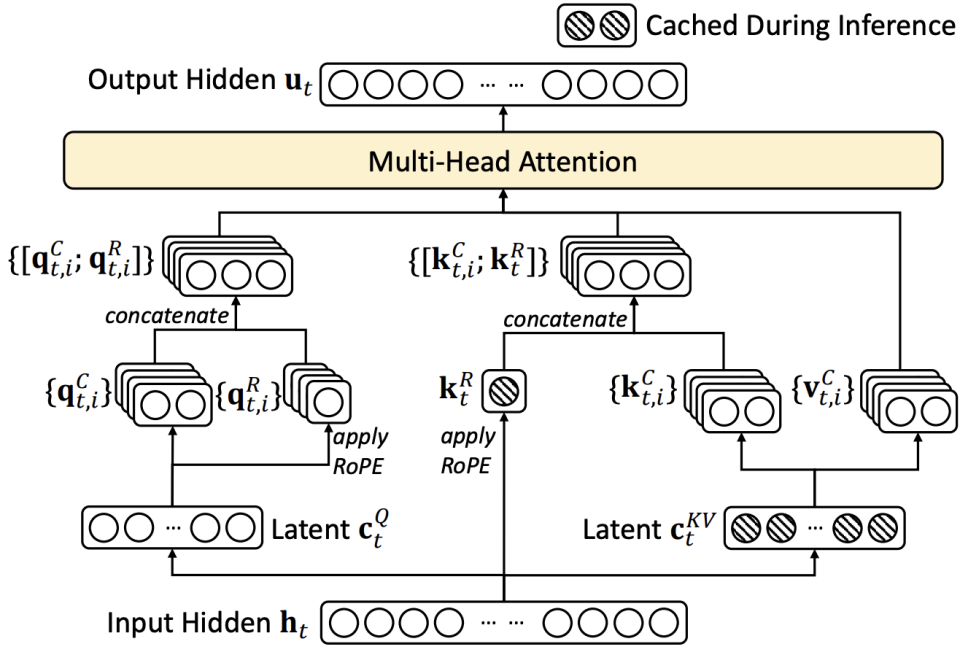 训练、推理场景下的等价性:缓存与效果的极限拉扯:从 MHA、MQA、GQA 到 MLA
训练、推理场景下的等价性:缓存与效果的极限拉扯:从 MHA、MQA、GQA 到 MLA
观察
- 模型的 attention 计算量只与
有关。 - KV 头数的压缩带来两个好处: a) 直接减少缓存量,容纳更长文本、更大 batch; b) 在容易 memory bound 的推理场景下提高计算密度。GQA 的计算密度为
,MQA 和 MLA 分别为 和 (由于 RoPE dim 的存在,实际略小)。 - 固定 KV cache 大小下,模型的理论 expressiveness 大小关系:GQA < MLA < MQA。基于此,已有 TransMLA 等工作。
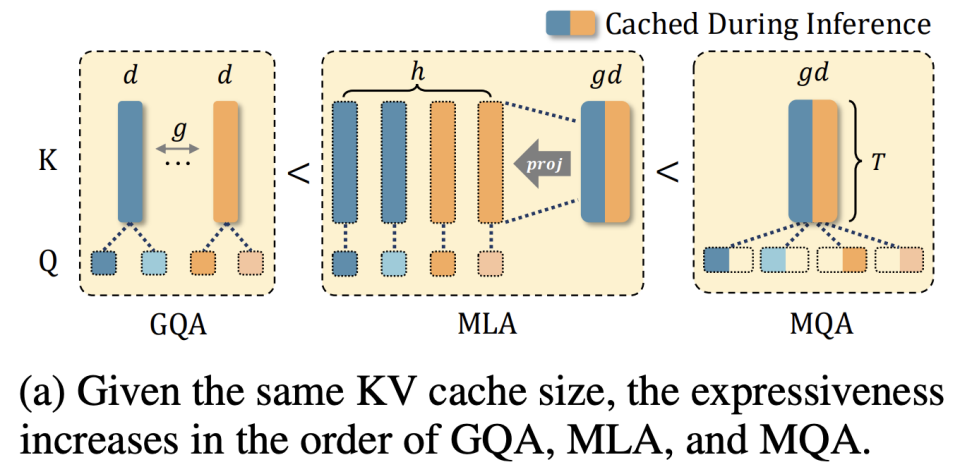
- 考虑并行性:
- GQA 可以受限地 TP(取决于
)。 - MLA、MQA 常采用 DP Attention(或 TP+DP,TP 会冗余复制 KV cache,而 DP 则会冗余复制 Attention 权重);序列并行不受影响。
- GQA 可以受限地 TP(取决于
- 考虑推理友好性,MQA、MLA 和
的 GQA 可以在推理场景下充分使用 tensor core。
Hardware-Efficient Attention for Fast Decoding
Tri Dao 团队
问题分析:解码阶段的瓶颈
- KV 缓存是主要瓶颈:自回归解码需缓存所有历史 token 的 KV 状态。随着批次大小(batch size)和上下文长度(context length)增加,KV 缓存大小线性增长,远超 HBM 容量。
- 内存访问主导延迟:解码阶段的计算(GEMV)量小,但加载庞大的 KV 缓存耗时长,导致 GPU 计算单元(如 Tensor Core)利用率极低(可低至 7%),形成内存墙(Memory Wall)。
- 并行性受限:解码的序列性限制了并行化机会,主要依赖注意力头的并行(TP)。现有优化方案(如 MQA、GQA、MLA)在并行扩展或模型质量上存在不足:
- MQA:所有查询头共享一个 KV 头,大幅减小缓存但牺牲质量,且 TP 时 KV 头需全设备复制,抵消内存节省。
- GQA:查询头分组共享 KV 头,是 MQA 与 MHA 的折中,但中等 TP 下每个设备的 KV 缓存仍较大,且大分组会降低质量。
- MLA:通过低秩投影压缩 KV 为单个潜在头缓存,算术强度高,但单潜在头设计在 TP 时需全设备复制缓存,限制了并行扩展和内存节省。
核心设计原则:算术强度与并行性
- 计算强度是关键指标:定义为计算量(FLOPs)与内存访问量(Bytes)之比。解码阶段需最大化算术强度(更多计算/字节),使计算从内存受限转向计算受限,充分利用 GPU 算力。
- 组大小是杠杆:
。增大 可提高算术强度、减小 KV 缓存,但过大会损害并行性(需跨设备复制权重和缓存)。 - KV 复用与并行友好:理想方案需同时实现高算术强度、高效跨设备并行(零冗余或低冗余),且不牺牲模型质量。
提出的解决方案:两种新型注意力机制
Grouped-Tied Attention (GTA)
- 核心思想:在 GQA 分组基础上,将 Key 和 Value 状态绑定(Tie)为一个共享状态,并仅对 Key 的部分维度应用位置编码(RoPE)。
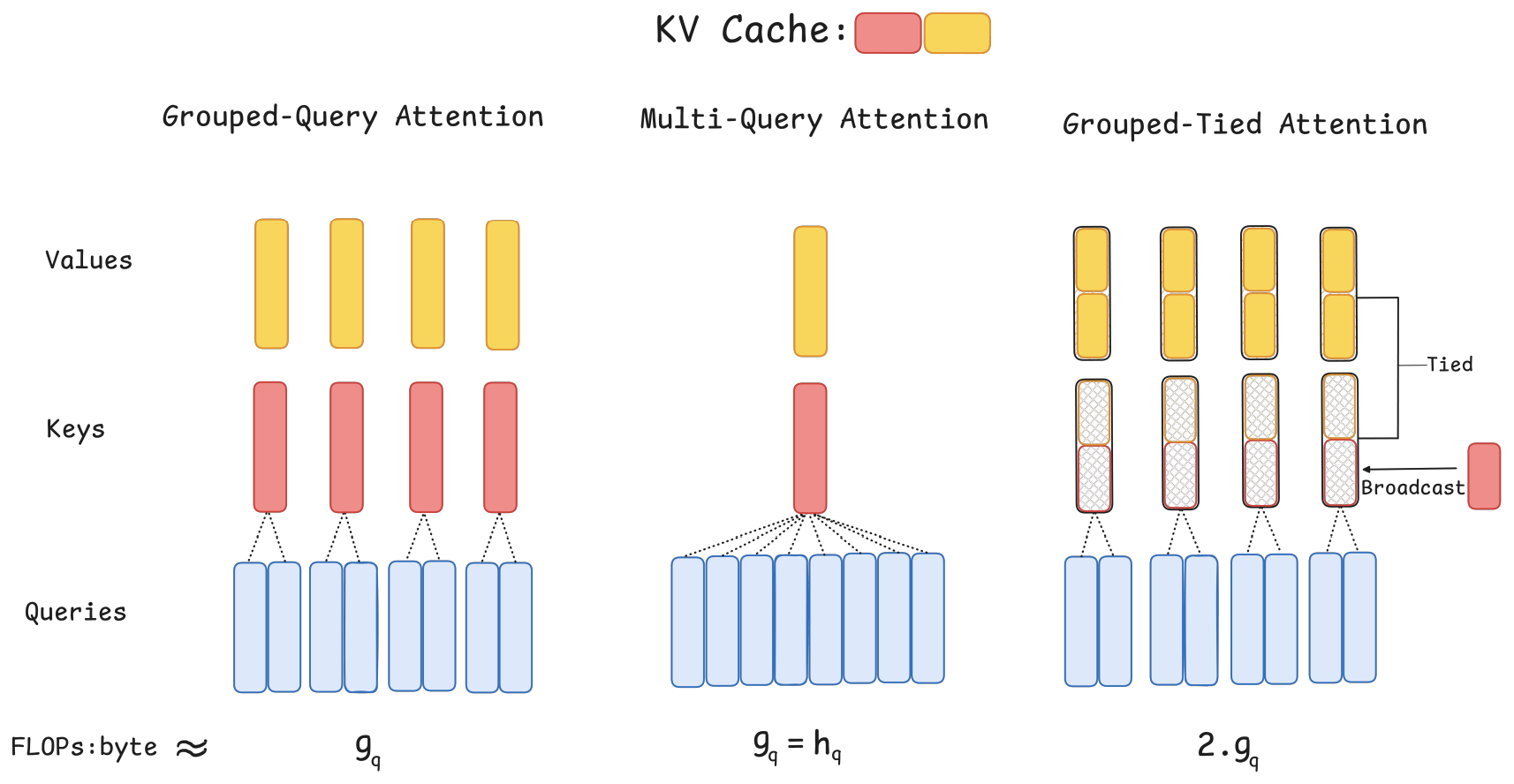
- 实现:
- 一个投影生成绑定 KV 状态(形状同单个 K 或 V 向量)。
- Value 路径使用整个绑定 KV 状态。
- Key 路径使用绑定 KV 状态的前半部分(不应用 RoPE) + 一个单独的单头投影(应用 RoPE)广播拼接而成。
- 优势:
- 相比同
的 GQA,KV 缓存减半(因 K 和 V 共享状态)。 - 算术强度翻倍(加载一次状态用于 K 和 V 计算)。
- 保持 GQA 的并行友好性。
- 实验证明质量匹配或优于 GQA(如 1.47B 模型,GTA-4 困惑度 10.12 vs GQA-4 的 10.20)。
- 相比同
Grouped Latent Attention (GLA)
- 核心思想:改进 MLA,将潜在表示分组(
组),每组服务一个查询头子集,并减小每组潜在头维度。 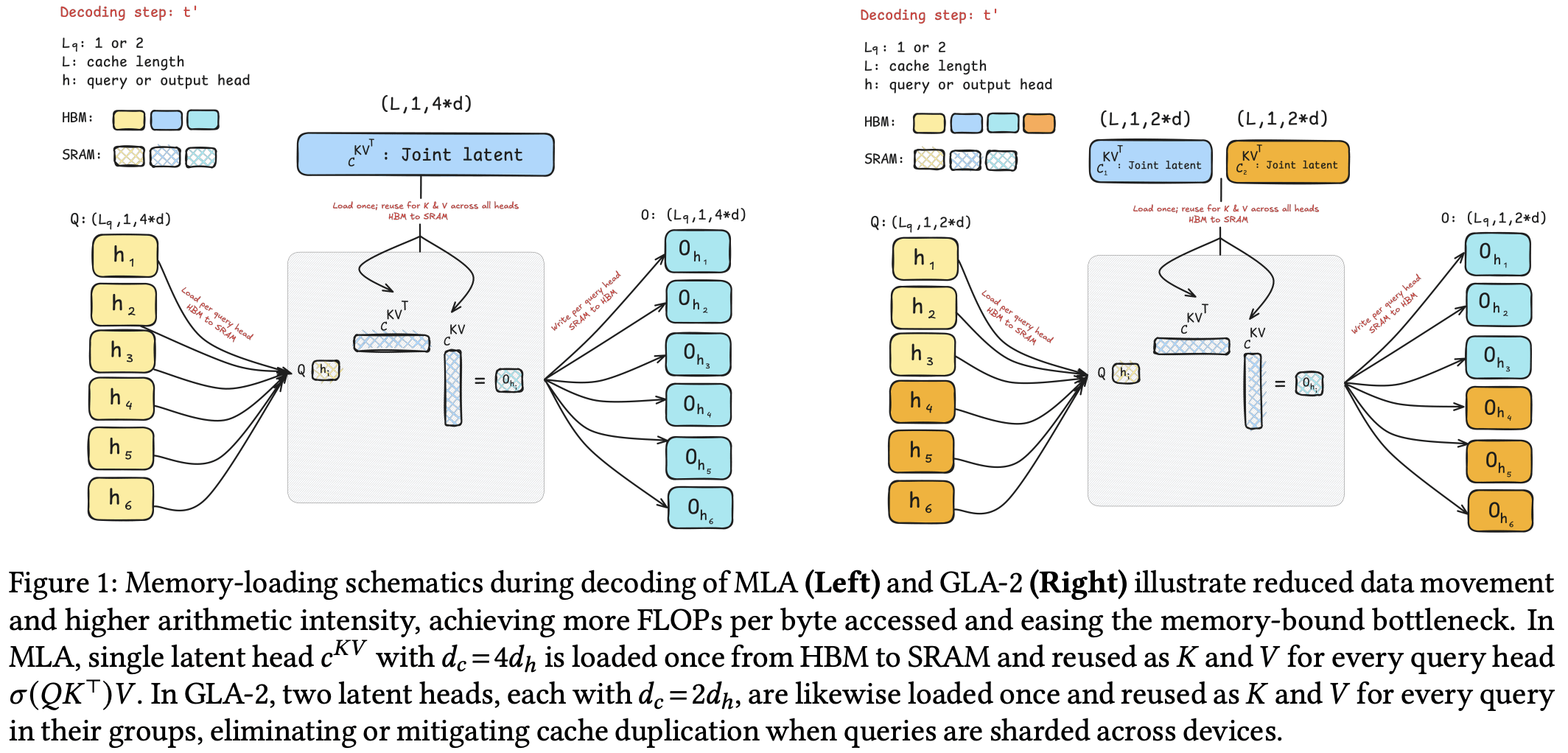
- 实现:
- 压缩 token 为
个潜在头(而非 MLA 的单个头),每个头维度 (MLA 为 )。 - 每个潜在头及其上投影矩阵重建其组内查询头的独立 K/V 特征。
- 解码时,潜在头可跨 TP 设备分片(如
时零冗余)。
- 压缩 token 为
- 优势:
- 与 MLA 总缓存相当(如 GLA-2 缓存
),但 TP 时每个设备缓存减半(如 TP=2 时,GLA-2 每设备缓存 vs MLA 的 )。 - 算术强度高(
),与 MQA 相当但质量更好。 - 并行友好:支持高效 TP 分片,避免 MLA 的缓存复制问题。
- 实验证明质量匹配 MLA(如 1.47B 模型,GLA-2 平均下游准确率 60.0% vs MLA 的 59.1%),且更容忍负载不均衡。
- 与 MLA 总缓存相当(如 GLA-2 缓存
小结
| 方案 | KV 缓存 | 算术强度 | 并行友好性 | 模型下游评测 |
|---|---|---|---|---|
| MHA | 最大 | 低 | TP 高效 | 49.65 |
| MQA | 最小 | 高(≈ | TP 需复制全量 KV 缓存 | 49.18 |
| GQA | 中等 | 中等(≈ | TP 受限 | 48.27 |
| MLA | 小 | 最高(≈ | TP 需复制全量缓存 | 49.24 |
| GLA | 小 | 最高(≈ | TP 受限 | 49.29 |
| GTA | 小于 GQA | 高(≈ | TP 受限 | 48.93 |
注:下游评测为我们固定了模型的参数量、train token 量,在 lm-evaluation-harness 上得到的 average acc(由于只 train 了一组,所以实际可能略有浮动,仅作参考)。